Ekstsentrilisus on 1,0.

Orbiidi ekstsentrilisus $ e $ leitakse apoapsi ja periapsi raadiuselt järgmiselt:

$$ e = \ frac {r_a-r_p} {r_a + r_p} $$

ja poolsuur telg $ a $ saab ka:

$$ a = \ frac {r_a + r_p} {2} $$

Kui viskate objekti horisontaalselt (kiirus on risti positsioonivektoriga), satute suletud orbiidile, kui viskate põgenemiskiirusest aeglasemalt - avatud paraboolne kui viskate selle täpselt põgenemiskiirusel või avatud hüperboolika, kui viskate suurema kui põgenemiskiirus.

On kiirus, mis tagab täiusliku ümmarguse orbiidi $ e = 0 $ . Võiksime seda sama hästi nimetada ka orbiidi kiiruseks. Kui ekstsentrilisuse võrrandis on $ r_a = r_p $ nagu ümmargusel orbiidil, näeme, et lugeja on null, samas kui nimetaja pole null, nii et kogu murdosa on samuti null.

Kui viskate ringkiirusest aeglasemalt, langeb objekt enne tagasi üles tulekut keskele lähemale. Mida madalamale objekt saab, seda madalam on periapse. Kui ekstsentrilisuse võrrand $ r_p $ väheneb, siis lugeja kasvab, samal ajal kui nimetaja kahaneb, nii et kogu murd suureneb. Aeglasemalt liikudes suurendame ekstsentrilisust.

Selle piirav juhtum on see, kui viskate selle nullkiirusel, st langete ära.

Tõelise punktmassi ümber gravitatsiooniväljale langenud objekti puhul jõuate apoapsini raadiuseni, mille juures objekti viskasite, ja periapsi nulli. See on väga imelik orbiit, sest objektil kulub keskpunkti jõudmiseks piiratud aeg, kuid see jõuab lõpmatu kiiruseni just siis, kui möödub keskusest, kus see teeb 180 ° pöörde ja kaldub tagasi ülespoole, kuni jõuab oma algsesse langusesse kõrgus nullkiirusel ja alustab teist tsüklit. Selle orbiidi aja arvutamiseks võite kasutada Kepleri kolmandat seadust, kuna sellel on endiselt täpselt määratletud $ a $ .

Sfääriliselt- kindla pinnaga sümmeetrilisel massil (nulltihedus väljaspool kindlat raadiust) on identne raskusväli keskpunktmassi omaga kõikjal väljaspool selle pinda. Seetõttu järgiks realistlikumal planeedil pinna kohale langenud objekt orbiiti, mis on identne punktmassi kohal sama raadiusega langenud orbiidile, kuni see vastu pinda satub. Kui see läbiks pinna (ütleme, et puurisite augu), pole pinna all olev gravitatsiooniväli mitte sama mis punktmassi oma.

Alati, kui olen pesapallimängu ja näete pop-flyi, see teeb mulle alati lõbuks, kui arvan, et rada, mida palli mööda minnakse, pole tegelikult parabool, vaid väga väljavenitatud ellipsi lõpp, mida jätkates moodustaks sama kuju Maa keskosa lähedal.

Sel juhul $ r_p = 0 $ . Ekstsentrilisuse murdosa loendur on võrdne väärtusega $ r_a-0 = r_a $ ja nimetaja on võrdne väärtusega $ r_a + 0 = r_a $ samuti. Ekstsentrilisus on täpselt 1,0.

"Aga Kwan!" Ma kuulen sind karjumas. "Kui $ e = 1 $ , kas see ei tee sellest paraboolset orbiiti?" Sel juhul ei. Paraboolsel orbiidil on $ e = 1 $ ja $ a = \ infty $ span >, samal ajal kui langusorbiidil on $ e = 1 $ , kuid kindlasti mitte lõpmatu $ a = r_a / 2 $ .

See juhtum on piiriks sellele, kui ellipsi muutub fookuste lahku liikudes järjest õhemaks. Selles piires on üks fookus keskel, üks langemispunktis ja ellipsil on null laiust, kuid lõplik pikkus.

Selles pildis tähistab liikumatu ring raadiusega kera 1 ja liikuv ellips tähistab orbiiti konstantse apoapsi raadiusega 2,0, kuid erineva ekstsentrilisusega.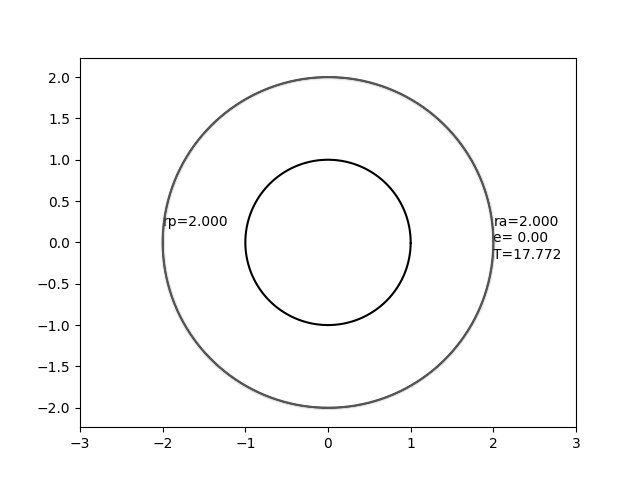

Pange tähele, et see pole ei mis juhtuks, kui puuriksite läbi maa augu ja viskaksite eseme maha. See kehtib ainult tõelise punktmassi kohta ja see ei võta arvesse suhtelisust (tõeline punktimass oleks ainsus ja objekt läbiks laskumistee sündmuste horisondi ja ei tuleks enam tagasi).

Radiaalse orbiidi ekstsentrilisus on $ 1 $ , olenemata selle energiast.

See on orbiitide klass, kus orbiidi tüüp ainuüksi ekstsentrilisusest ei saa järeldada. Traditsioonilise paraboolse orbiidiga $ e = 1 $ on nurga impulss $ L $ täpselt määratletud väärtus, kuid poolteljev telg $ a $ pole määratletud. Vertikaalselt piiratud vabalangemisorbiidi korral on pool-suurtelg $ a $ täpselt määratletud väärtus ja nurgamoment $ L $ on $ 0 $ .

Nurkmomenti ekstsentrilisuse ja poolteljega teljega seotud võrrand näitab, kuidas ekstsentrilisust saab arvutada nurkkiiruse põhjal. $$ l = \ sqrt {\ mu a (1-e ^ 2)} $$ paraboolse orbiidi korral $ a \ rightarrow \ inf $ , seega nurkkiiruse määratlemine selle valemi abil ei toimi. Kuid radiaalsete orbiitide puhul, kus objekt ei liigu täpselt põgenemiskiirusel, on see valem hästi määratletud. See tähendaks, et radiaalse trajektoori ekstsentrilisus, olenemata energiast, on $ 1 $ . Orbiidi ekstsentrilisust käsitlev vikipeedia artikkel kinnitab seda.

Radiaalsed trajektoorid klassifitseeritakse elliptilisteks, paraboolseteks või hüperboolseteks orbiidi energia, mitte ekstsentrilisuse põhjal. Radiaalsetel orbiitidel on null nurk ja seega ekstsentrilisus võrdne ühega. Energia konstantsena hoidmine ja nurkkiiruse vähendamine kipuvad elliptilised, paraboolsed ja hüperboolsed orbiidid kumbki vastavat tüüpi radiaalsele trajektoorile, samas kui e kipub 1 (või paraboolsel juhul jääb 1).

Mitu definitsiooni võimaldavad radiaalsel orbiidil olla ka ekstsentrilisus.

$$ e = \ frac {r_a-r_p} {r_a + r_p} $$

$$ e = \ sqrt {1 + \ frac {2 \ epsilon l ^ 2} {\ mu ^ 2}} $$

koos $ \ epsilon $ on spetsiifiline orbitaalenergia. Kuid sisendina ekstsentrilisusega muu kasutamine võib viia määratlemata tulemusteni. Nimelt nurjub parameetriline määratlus $ \ theta = 0 $ :

$$ r = \ frac {a (1-e ^ 2)} {1-e \ cos \ theta} $$

Nii et koju võib tuua, et radiaalse orbiidi ekstsentrilisus on $ 1 $ olenemata selle energiast. Kuid ekstsentrilisuse kasutamine orbiidi arvutuste tegemisel võib viia määratlemata tulemuseni.

Ma olin juba varem maininud, et koonusjagu on joon, kuid arvan, et see on vale, kuna orbiiti saab piirata (ja see on küsimuses) ja see on joone segment. Nii et ma olen uudishimulik koonusjaotise kohta piiratud orbiidilt (ja positiivse energia radiaalorbiidilt).